Prawie odkryty zbiór
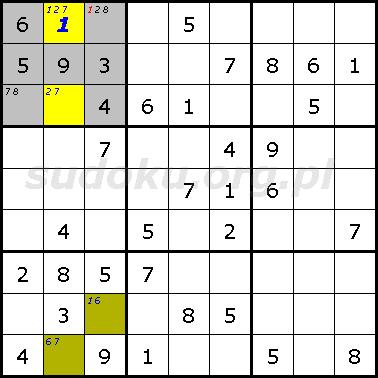
Prawie odkryty zbiór (ang. Almost Locked Set) występuje wtedy, gdy w N pól danego obszaru można wpisać dokładnie N+1 kandydatów. Najmniejszym prawie odkrytym zbiorem jest pole z dwoma kandydatami. Pojedynczy prawie odkryty zbiór nie pozwala na dokonanie jakiejkolwiek eliminacji. Jedną z technik wykorzystującą dwa prawie odkryte zbiory jest ALS-XZ. Aby użyć tej techniki musi istnieć liczba X, która nie może wystąpić jednocześnie w obydwu zbiorach. Zatem jeśli liczba X będzie wpisana w pole jednego ze zbiorów, drugi automatycznie stanie się odkrytym zbiorem. Jeśli więc istnieje liczba Z, która występuje w obydwu zbiorach, to można wyeliminować tę liczbę z pól, które "widzą" wszystkie pola obydwu zbiorów zawierające liczbę Z, ponieważ albo zbiór pierwszy będzie zawierał tę liczbę, albo zbiór drugi będzie zawierał tę liczbę, albo obydwa.Na poniższym diagramie sudoku w pola lewego górnego kwadratu R1K2 i R3K2 można wpisać trójkę liczb 1, 2 i 7. Jest to pierwszy prawie odkryty zbiór. W pola lewego dolnego kwadratu R8K3 i R9K2 można wpisać trójkę liczb 1, 6 i 7. Jest to drugi prawie odkryty zbiór. Liczbą X jest liczba 7 ponieważ nie może wystąpić jednocześnie w obydwu zbiorach. Liczbą Z jest liczba 1, która występuję w obydwu zbiorach. Używając tej techniki można ją wyeliminować z pola R1K3, pole to widzi wszystkie pola obydwu zbiorów zawierające liczbę 1. Dzięki tej eliminacji w lewym górnym kwadracie liczbę 1 można wpisać tylko w pole R1K2.
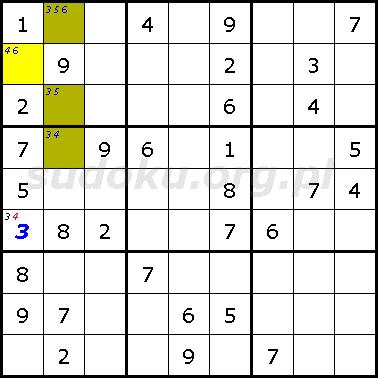
Na kolejnym diagramie sudoku w pole R2K1 można wpisać parę liczb 4 i 6. Jest to pierwszy prawie odkryty zbiór. W pola drugiej kolumny R1K2, R3K2 i R4K2 można wpisać czwórkę liczb 3, 4, 5 i 6. Jest to drugi prawie odkryt zbiór. Liczbą X jest liczba 6 ponieważ nie może wystąpić jednocześnie w obydwu zbiorach. Liczbą Z jest liczba 4, która występuję w obydwu zbiorach. Używając tej techniki można ją wyeliminować z pola R6K1, pole to widzi wszystkie pola obydwu zbiorów zawierające liczbę 4. Dzięki tej eliminacji w pole R6K1 można wpisać tylko liczbę 3.